If you saw our video of words derived from numbers earlier this month, you’ll know that March 14 was Pi Day (or rather, the once-in-a-century Rounded-Up Pi Day), because when it’s written out numerically the date “3.14.16” forms the first few digits of pi.
Besides our mathematically-themed video, however, over on the HaggardHawks Twitter feed we marked Pi Day with this fairly remarkable fact:
The FEYNMAN POINT is a series of six consecutive 9s in the 762nd-767th decimal places of pi. #PiDay pic.twitter.com/5ZyAZQs66x— HaggardHawks Words (@HaggardHawks) 14 March 2016
Now. We’re not mathematicians here at HaggardHawks, and frankly the very idea of discussing the irrationality of an approximation of the mathematical constant representing the ratio of the circumference of a circle to its diametzzzzzzzzzzzzzzz…
Only joking, mathematicians, we love you really. But even dusty, bookish old wordsmiths like us can find some interest in mathematics every so often, and the Feynman Point is one of those times. So we thought you might like to know a little bit more about the point behind The Point.
The “Feynman” of the Feynman Point is the American theoretical physicist Richard Feynman. In a lifetime of achievement and accomplishment, Feynman did everything from helping develop the atomic bomb to assisting in the commission that investigated the Challenger disaster in 1986. He was also jointly awarded the 1965 Nobel Prize for Physics for his “fundamental work in quantum electrodynamics”, including his groundbreaking work on quantum path integral formulation challenging the existing notion of a unique quantum trajectory by replacing it with a functional integralzzzzzzzzzz…
Only joking, physicists, we love you as well. But long story short, Richard Feynman was a brilliant scientist—and he was also very interested in π.
According to the story, during a lecture at the California Institute of Technology, Feynman joked to his students that he would one day like to memorize pi up to the point, 762 decimal places in, that there are six consecutive nines. Why? Well, he wanted reach that particular repdigit and then state “...999999, and so on”, implying that the famously irrational π suddenly, 762 places in, becomes nothing more than an infinite chain of 9s.
Regrettably there’s little evidence that Feynman ever actually made that joke (and in fact the earliest account of it credits it to fellow scientist Douglas Hofstader), but it’s Feynman’s name that has ended up being attached to these six consecutive 9s, and its his name that has remained in place ever since.
Incidentally, another six consecutive 9s crop up in the 193,034th–193,039th decimal places of pi. Anyone fancy memorizing up to there? You could get your name in the dictionary if you do...
Incidentally, another six consecutive 9s crop up in the 193,034th–193,039th decimal places of pi. Anyone fancy memorizing up to there? You could get your name in the dictionary if you do...

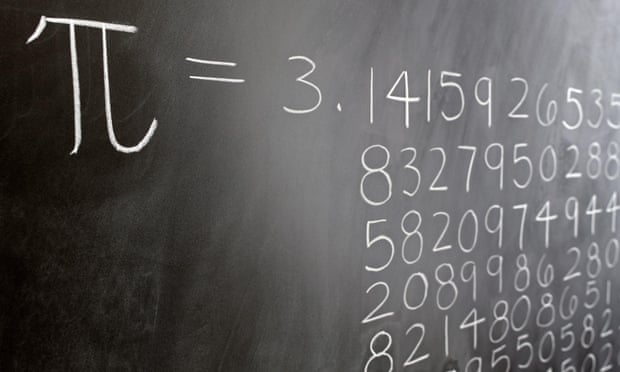
The Feym of the Feymous Feynman point is hightly overrated for several reasons: First a 999999 was bound to crop up within the first million digits or so (why would we expect it to wait till the millionth digit. The chance of 999999 appearing somewhere within any randomly chosen segment of 678 is almost one percent. Since the digits of Pi are not really randomly distributed but just appear so, we really should expect 999999 to appear exactly where it is. God didn't PLAN for it to be there. If GOD wanted us to be practical he would have placed it at digit 7 rather than at digit 762 as a hint that we could safely represent it a 355/113 and round it off to be 3.141593 and avoid trying to get it any closer than that. The second reason it is highly overrated is that in base 2-8 it doesn't appear at all (888888 is the big deal in octal) and FFFFFF is the big deal in hexadecimal. So lets just pretend that Pi is rational. It is the rational thing to do because it easier to memorize 3.1415930000000... to a hundred digits (or 3.141592999999... if you prefer.) And the error you get on the circumference of a circular swimming pool with a diameter of a hundred meters would be about 3 hundreths of a millimeter if you just use 355/113 Chances are it will be off by a thousand times more than that just due to construction errors. Enough said!
ReplyDeleteReally? Obviously you don't understand the term quip.
Delete'====(The computer language I used here is called "PARI/GP")
ReplyDelete'=================================================================='
'======== Exhaustive search through all number bases 2 to 1000
'======== to find base with best approximation to Pi when
'======== rounding after any of its first 10000 digits:
\\abbreviated variables I used to save space:
\\RP=RoundingPoint in number expressed in the particuluar base being tested
\\RP10=RP in number after converting to base 10
\\EFR=ErrorFromRounding (expressed in base 10 digits)
\\This is the main search function I made:
ExhaustiveSearch()={
Min=100;
for(Base=2,1000,
for(RP=1,10000*log(10)/log(Base),
EFR=abs(round(Pi*Base^RP)-Pi*Base^RP);
if(EFR<=Min,
Min=EFR;
RP10=round(RP*log(Base)/log(10));
print(Base,"\t",RP,"\t",RP10,"\t",EFR);
)))
}
(12:45:15) gp > \p30000
realprecision = 30016 significant digits (30000 digits displayed)
(12:46:00) gp > default(format,"g.12")
(12:46:01) gp >
(12:46:02) gp > \p
realprecision = 30016 significant digits (12 digits displayed)
(12:46:03) gp > ExhaustiveSearch()
2 1 0 0.283185307180
2 3 1 0.132741228718
2 6 2 0.0619298297468
2 10 3 0.00912272405172
2 95 29 0.00671730244541
2 188 57 0.00199792756645
2 644 194 0.000622884136028
2 2931 882 0.000538723428992
2 4266 1284 0.000410737154421
2 5211 1569 0.000319758275984
2 8374 2521 3.32956963894 E-5
2 11790 3549 7.91594467615 E-6
4 5895 3549 7.91594467615 E-6
5 7939 5549 2.19245712054 E-7
10 761 761 1.62702195005 E-7
314 760 1898 1.49047408232 E-7
700 56 159 1.39659347874 E-7
(12:56:46) gp >
There one can notice that base 10 gives
an exceptionally good Pi approximation at only the 761th digit,
and the next best base to use is 314 (also at its 760th digit)
a base whos own digits happen to be
a common approximation that people use for Pi itself.
However of all possible bases up to 1000 one can see that
base 700 has by far the best digit-rounded approximation
to Pi when rounded at its 56th 700-based digit:
in base 700 Pi to the 56th 700-based digit is:
[3, 99, 80, 280, 126, 636, 384, 498, 226, 595, 189, 5, 420, 473, 473, 437, 18, 641, 474, 213, 193, 521, 600, 656, 302, 475, 500, 240, 497, 98, 465, 319, 180, 516, 542, 214, 445, 210, 661, 193, 271, 414, 147, 32, 163, 509, 142, 544, 181, 113, 313, 540, 25, 228, 629, 304, 5]
which in base 10 is:
6647220931122939479128537740915757237246006043994211373938106113509869531847715607364950177872853012448253864239447228161300041621772396211640760800881012422805.
number of base 10 digits of that is:
159.8226401134925163742353787694785257087317325185225
but it's accurate to
2.101018595906417996765 x 10-167
which means accuracy in base 10 digits is:
-166.677570103679814749882876152237
so the free gain in accuracy by using base 700 at the 56th base-700 digit point is:
6.85492 base 10 digits get added for free.
which means an added accuracy of one part in:
7160279.74525
which is 1.3965934783 x 10^-7
'=============== The End ======================